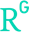Finding discrepancies between the predictions of fundamental theories and experimental observations is the main driver to develop physics further – the route to more advanced theories (“new physics”) that fix the discrepancies. In that sense, quantum electro-dynamics (QED) is currently seen as the most advanced fundamental theory, serving as the blueprint for any other quantum field theory. Progress is expected to come from ever more precise testing through comparison of theoretical predictions and experimental data. A good test compares values that can be both computed and measured with high accuracy. Some QED predictions excel in that respect, such as for the transition frequencies of atomic hydrogen [1] and the gyromagnetic ratio of the electron [2].

Most theories, including QED, depend on parameters that have to be adjusted to the experimental data. This means that the number of measurements must exceed the number of parameters, otherwise the theory can always be made correct. The test is passed if the various values for the parameters agree within their respective uncertainties. Precision-spectroscopy determinations and computations of transition frequencies of atomic hydrogen provide the best test for QED. The QED expression for the hydrogen energy levels effectively comes with two parameters: the Rydberg constant R∞ and the rms proton charge radius rp. Other parameters, such as the fine structure constant and the electron-to-proton mass ratio, appear as well, but can be better determined from other experiments. 

Until 2010, the 15 distinct measurements of transition frequencies in atomic hydrogen as used by CODATA [3] gave 13 value pairs for R∞and rp that were consistent with QED. This situation changed, however, when the frequency of a particular transition (the 2s-2p transition) in muonic hydrogen was measured [4]. Muonic hydrogen is just like regular hydrogen but with the electron replaced by its big brother, the muon. With this replacement the proton-radius term in the theoretical description and thus the sensitivity to this parameter – is seven orders of magnitude larger than for regular hydrogen. The result was a much more precise but also significantly smaller value of rp. This meant the QED test failed. The discrepancy between the “small” and “large” charge radius amounts to four combined standard deviations.

In addition to the hydrogen data the CODATA team uses data for the proton charge radius obtained from electron-proton scattering. This increases the discrepancy to 5.6σ and triggered intense discussions in the community whether or not this should be seen as a hint of new physics. It should be mentioned though that electron-proton scattering experiments are notoriously difficult to evaluate and values for rpfrom different groups disagree. The cleaner way to test QED is to compare only quantities that should obey the same physics, namely various transitions in regular and muonic hydrogen. After publication of the muonic hydrogen results, our group re-measured one of the broader hydrogen lines with better accuracy. Our motivation was that the discrepancy with the muonic value only shows up when all available hydrogen data is averaged. Our latest result for the 2s-4p transition frequency is as accurate as the previous “world data” and supports the “muonic” proton radius

Meanwhile Hélène Fleurbaey and her team at the Laboratoire Kastler Brossel, Paris have re-measured the 1s-3s transition frequency with a significantly improved accuracy and again find the “large” charge radius [5]. At our lab we have also been working on this transition with a different method. We hope to be ready to report some preliminary results. This would provide a unique opportunity to compare two highly accurate measurements obtained at different labs. In case of disagreement this would be a strong hint for a measurement problem causing the “proton radius puzzle”.

With Lothar Maisenbacher, Axel Beyer, Vitaly Andreev, Alexey Grinin, Arthur Matveev, Ksenia Khabarova, Nikolai Kolachevsky, Randolf Pohl, Dylan Yost and Theodor Hänsch

[1] A. Beyer et al. Science 358, 79 (2017).

[2] G. Gabrielse et al. PRL 97, 030802 (2006).

[3] P. J. Mohr et al. RMP 88, 035009 (2014).

[4] R. Pohl et al. Nature 466, 213 (2010).

[5] H. Fleurbaey et al. PRL 120, 183001 (2018).