This website uses cookies to ensure a better user experience.
To get more information, please read our Cookie Statement.
Convergence of Nonperturbative Approximations to the Renormalization Group
Ivan Balog, together with a collaboration of scientists from Sorbonne Université, Visage Technologies AB, CEA Saclay and the University of Montevideo, has published an article in the prestigious journal Physical Review Letters. Authors have studied the convergence properties of the derivative expansion, an approximation which is often used for calculating the long wavelength properties in statistical physics, condensed matter and high energy physics.
Convergence of Nonperturbative Approximations to the Renormalization Group
Ivan Balog, Hugues Chaté, Bertrand Delamotte, Maroje Marohnić, and Nicolás Wschebor,
Physical Review Letters 123, 240604 (2019).
DOI: https://doi.org/10.1103/PhysRevLett.123.240604
Wilsonian renormalization group (RG) is an extraordinary means of understanding quantum and statistical field theories. A modern incarnation of this method was proposed by Christoff Wetterich a quarter of century ago, under the name of nonperturbative renormalization group (NPRG). Nonperturbative approach to the RG is versatile, allowing us to treat equilibrium and nonequilibrium problems, with access to both universal and nonuniversal quantities. Just to mention a few successes with problems previously unsolved: universality of the random field Ising model, strong coupling solution of the Kardar-Parisi-Zhang equation, criticality in glassy problems, the phase diagram of the reaction-diffusion systems and many others.
The starting point of the approach is in the exact nonperturbative flow equation of the effective average action, which in principle allows gradual summation over short towards long wavelength degrees of freedom, which at the end leads to summation over all of them, giving the exact free energy of the system under consideration. The problem is in the fact that the exact flow equation is impossible to solve exactly for almost any relevant problem and hence the approximations need to be made. One of the most commonly used approximations is the derivative expansion, which is the subject of the present article, in which one does an expansion around the long wavelength limit.
Despite numerous successes, the nonperturbative renormalization group is very often criticized. Two main points which are usually raised are: a) the apparent lack of a small parameter which should control the convergence and b) the residual dependence of the results on the infrared regulator function, which has to be introduced in the procedure of resummation successive wavelengths.
The present article gives clear and rigorous answers to both criticisms. It gives analytical and numerical arguments which show the convergence of the derivative expansion and also reveal when this convergence is expected to be fast. Namely the rapidity of the convergence of results depends on the magnitude of the anomalous dimension and is rapid when this dimension is small, which is often the case. An extensive study was made of the dependence of the results on the regulator function and the conclusion was obtained that if one respects several basic principles in choosing it, any choice is good enough to ensure a (fast) converging result. Additionally for the first time the error estimates of the critical exponents determined by the NPRG are provided.
The results of the paper show that the NPRG, which is well known for its versatility in the studies of critical phenomena, can even be thought of as quantitatively precise, since it was shown on the example of φ4 theory that it is possible to obtain results which compare in accuracy to the Monte Carlo results and far supersede any other renormalization group approach.
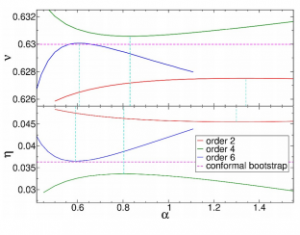
Exponent values ν(α) and η(α) at different orders of the derivative expansion. Vertical lines indicate αopt. Local potential approximation (s = 0) results do not appear within the narrow ranges of values chosen here.