Kolega Ivan Balog, zajedno s grupom znanstvenika sa Sveučilišta Sorbonne, tvrtke Visage Technologies AB, CEA Saclay te Sveučilišta u Montevideu, objavio je rad u prestižnom časopisu Physical Review Letters. Autori su proučavali konvergenciju derivacijskog razvoja, aproksimacije koja se često koristi za analitičke račune dugovalnih svojstava sustava u statističkoj fizici, fizici kondenzirane materije, ali i fizici visokih energija.

Convergence of Nonperturbative Approximations to the Renormalization Group

Ivan Balog, Hugues Chaté, Bertrand Delamotte, Maroje Marohnić, and Nicolás Wschebor,
Physical Review Letters 123, 240604 (2019).

DOI: https://doi.org/10.1103/PhysRevLett.123.240604

Wilsonova renormalizacijska grupa se pokazala kao izniman alat za razumijevanje kvantnih i statističkih teorija polja. Modernu inkaranciju ove metode predložio je pred četvrt stoljeća Christoff Wetterich pod imenom neperturbativna renormalizacijska grupa (NPRG). Ovaj alat pokazuje se kao nevjerojatno općenit jer omogućuje opis ravnotežnih kao i neravnotežnih problema te pristup univerzalnim i neuniverzalnim veličinama koje opisuju sustav. Do sada je NPRG uspješno primjenjena u mnogim problemima koji su do tada bili neriješivi standardnim metodama perturbativne renormalizacijske grupe, kao što su na primjer: Isingov model u nasumičnom polju, Kardar-Parisi-Zhang jednadžba, staklasti fenomeni, reakcijsko difuzijski problemi te mnogi drugi.

Ishodište pristupa jest egzaktna neperturbativna jednadžba toka za efektivno djelovanje, koja u principu omogućuje postupnu sumaciju preko kratkovalnih stupnjeva slobode prema
dugovalnima te na taj način, kada su svi stupnjevi slobode prosumirani, daje egzaktnu slobodnu energiju modela koji se proučava. Problem jest što egzaktnu jednadžbu toka gotovo
nikad nije moguće riješiti egzaktno te se stoga moraju uvesti aproksimacije, kao što je derivacijski razvoj koji je predmet ovoga rada, u kojemu se radi razvoj efektivne teorije oko dugovalne granice. Ova vrsta aproksimacije najčešće se koristi za proučavanje fizike faznih prijelaza.

Unatoč brojnim uspjesima, neperturbativna renormalizacijska grupa je često meta kritika. Dvije najčešće su: a) nedostatak očitog malog parametra koji kontrolira konvergenciju
razvoja te b) rezidualna ovisnost rezultata o infracrvenom regulatoru, funkciji koju je nužno uvesti pri postupku postupnog sumiranja po brzim stupnjevima slobode.

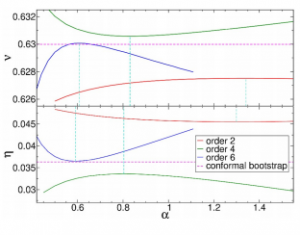
Ovaj članak daje jasne rigorozne odgovore na obje kritike. Izneseni su analitički te numerički argumenti koji pokazuju da derivacijski razvoj konvergira, te također kada
je ta konvergencija vrlo brza. Naime brzina konvergencije ovisi direktno o kritičnom eksponentu renormalizacije polja koji je u mnogim slučajevima znantno manji od 1. Također
provedena je ekstenzivna studija rezultata u ovisnosti o regulacijskoj funkciji te je zaključak da ako se poštuje par temeljnih principa u njenom odabiru, da je bilo koji izbor dovoljno dobar te da vodi na (brzo)konvergirajući rezultat. Također, po prvi puta za neperturbativne metode renormalizacijske grupe, temeljeno na analitičkim argumentima konvergencije, u članku su navedene granice preciznosti procjena za kritične eksponente.

Ovaj rezultat pokazuje da se metoda neperturbativne renormalizacijske grupe, već prije znana kao najopćenitiji okvir za proučavanje kritičnog ponašanja, sada nameće i kao kvantitativni alat, jer je na primjeru φ⁴ teorije pokazano da se rezultati za kritične eksponente koje je moguće dobiti s njom mjere s Monte Carlo simulacijama, te su bolji od bilo kojeg drugog pristupa renormalizacijske grupe.